https://arxiv.org/abs/2310.11453
Microsoft가 1저자인 논문이고, 2023년 10월에 아카이브에 올라온 논문입니다.
Abstract
이 논문에서는 LLM에 맞는 1-bit Transformer architecture, BitNet을 제안합니다.
BitNet은 Linear layer를 scratch부터 학습하는 1-bit weight의 BitLinear로 대체한 architecture입니다.
이 방법은 memory footprint와 에너지 소모를 줄이면서, 8-bit quantization SOTA와 FP16 Transformer baseline와도 경쟁력있는 성능을 보였습니다.
또한, full-precision Transformer처럼, scale을 키우면 성능이 더 좋아지는 scaling법칙을 따르는 것도 확인했습니다.
Introduction
모델의 큰 파라미터를 접근하고 처리할때, 메모리 대역폭에 병목이 생기면서 전반적인 inference 속도에 제한이 생깁니다.
** 메모리 대역폭 : 데이터를 얼마나 빠르게 읽고 처리하느냐, input x에 대한 추론 연산을 하기 위해서는 weight를 읽어야함
분산시스템이나 multi-device 환경에 배포할때에도 device간의 통신 overhead가 inference latency과 에너지 사용에 영향을 줍니다. 이때, quantization은 memory footprint와 계산 자원을 효과적으로 줄일 수 있는 방법입니다.
** Memory footprint : 전체 메모리 사용량
대부분의 Quantization 방법들은 학습후에 quantization하는 PTQ(Post-Training-Quantization) 방식을 사용합니다.
하지만, precision이 내려갈수록 큰 정확도 손실이 발생합니다.
** Precision : 정밀도! 32bit, 16bit, 8bit, 4bit, 3bit, 2bit, 1bit
반대의 개념은 QAT(Quantization-aware training)인데, 학습중에 quantization을 하면서 최적화하는 방법입니다.
PTQ에 비해서 정확도가 높지만, 낮은 precision에서 모델이 수렴하기 어려워지고, neural language models에서 scaling 법칙을 따르는지에 대한 조사가 덜 됐습니다.
또한, 기존 방법들은 CNN이나 기계번역, BERT-pretraining에 초점을 두었기 때문에 LLM과는 구조적인 차이가 있습니다.
(Encoder-Decoder Architectures, Bidirectional Encoder, Unidirectional Decoder)
제안한 BitNet은 PagedAttention, FlashAttention, and speculative decoding와도 함께 사용할 수 있습니다.
Method

위 그림에서 볼 수 있듯, BitNet은 Transformer와 동일한 구조를 사용하고, 다른 것은 nn.Linear대신 1bit weight인 BitLinear를 사용한다는 것입니다.
그 외에 다른 것들은 1-bit가 아닌, 8-bit를 사용했습니다.
- Residual connection과 layer normalization은 computation cost가 매우 작아서 압축할 필요가 없다.
- Input/Output embedding은 precision을 보존해야, language model이 sampling을 할때 high-precision 확률을 쓸 수 있다.
Weight Quantization
우선, weight를 Sign함수(0이하는 -1, 0보다 크면 +1)로 이진화합니다.
기존 연구(LOP+22)를 따라서, weight를 0을 중심으로 $\alpha$로 centralize했는데, capacity를 올리는 효과가 있다고 합니다.
scaling factor $\beta$는 이진화 후에 원래 값과의 l2 error를 줄이기 위해 사용합니다.

Activation Quantization
Activation은 8-bit precision으로 학습중에는 모든 activation에 대해서, 추론에는 토큰별로 quantization을 합니다.
기존 연구(DLBZ22)에 따라서, [$-Q_{b}$, $Q_{b}$] ($Q_{b} = 2^{b-1})$범위로 만드는 absmax quantization를 사용합니다.

** ϵ : clipping에서 발생할 수 있는 overflow를 방지, Floating에서 발생할 수 있는 오차범위를 조정하는 것으로 이해함.
ReLU같은 non-linear function전에는 [0, $Q_{b}$]로 scaling합니다.
- 제일 작은 값으로 빼서, 해당 범위로 rescaling해서 모든 value에 대해 non-negative로 만듭니다.
위의 수식들을 사용해서 matrix multiplication을 다시 쓰면 아래와 같습니다.

$W$와 $x$의 원소들이 평균이 0인 서로 독립이고, 같은 분포라고 가정할때, output $y$의 분산은 아래와 같이 추정할 수 있습니다.

일반적인 full-precision에서 초기화방법(Kaiming initialization or Xavier initialization)을 사용하면 Var($y$)이 1이 되고, 학습 안정성에 좋다고 합니다.
논문의 저자들은 quantization 이후의 분산값을 1로 보존하기 위해 activation quantization전에 LayerNorm을 사용합니다.

이를 사용해서 전체적으로 다시 표현하면 아래와 같습니다.

Model parallelism with Group Quantization and Normalization
현재 LLM은 너무 크기 때문에 여러 device에서 학습 및 추론하는 편입니다.
하지만 quantization에서 사용하는 파라미터 ($\alpha$, $\beta$, $\gamma$)등은 전체 $w$에 대해서 계산하기 때문에, 각 device끼리 공유를 하기 위해서는 communication cost가 필요하고 병목이 생기는 문제가 있습니다.
이를 해결하기 위해서, 나눠진 weight와 activation에서 독립적으로 계산해서 device간의 통신 cost를 없애는 방법을 선택했습니다.
Experiments
Comparison with FP16 Transformers



Comparison with Post-training Quantization

Conclusion and Future Work
- Scalable하고 Stable한 1-bit Transformer 아키텍처인 BitNet을 제안했다.
- Baseline과 비교했을때 perplexity와 downstream task performance에서 경쟁력있고, memory footprint와 energy consumption이 낮다.
- FP Transformer와 동일하게 Scaling 법칙을 따라서, 더 큰 larger language model에 적용해도 좋을 것이다.
- 추후에 Model size와 training step을 올려볼거고, ResNet같은 모델에 적용해보고 싶다.
'Papers > Compression' 카테고리의 다른 글
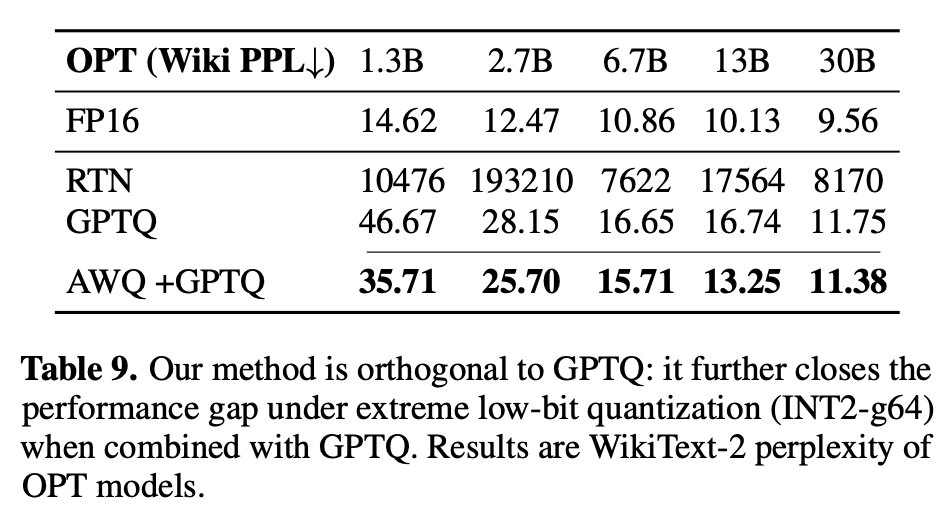
| AWQ: Activation-aware Weight Quantization for on-device LLM compression and acceleration (3) | 2025.07.14 |
|---|---|
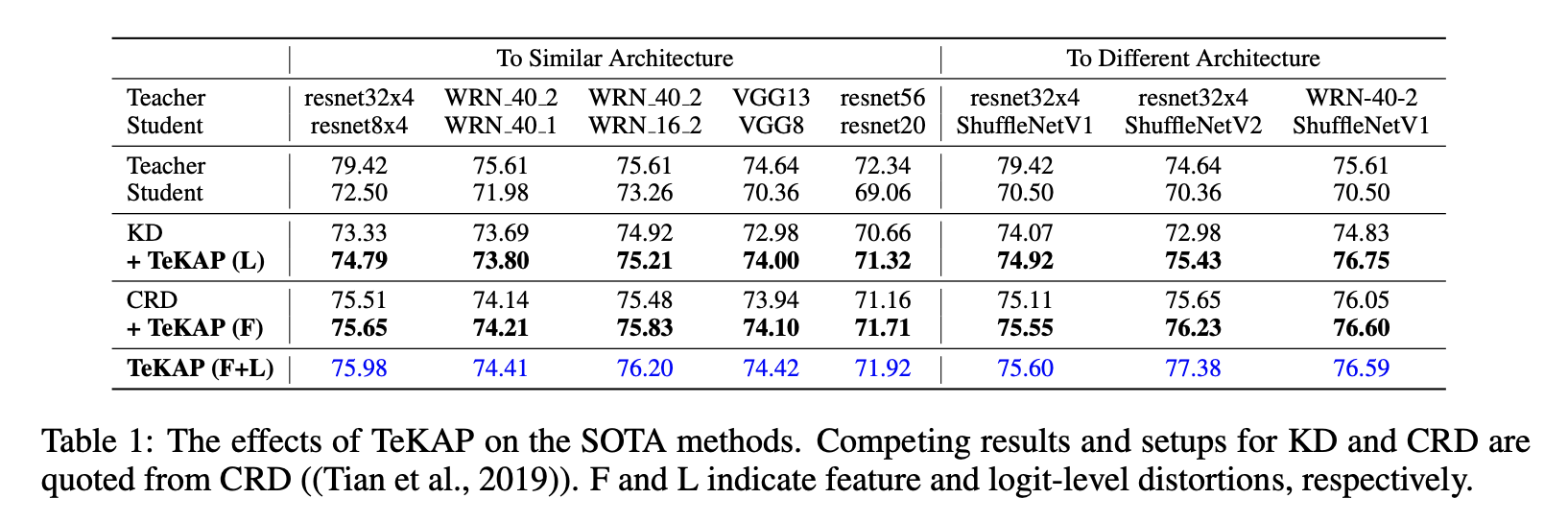
| SINGLE TEACHER, MULTIPLE PERSPECTIVES: TEACHERKNOWLEDGE AUGMENTATION FOR ENHANCED KNOWLEDGE DISTILLATION (0) | 2025.03.16 |
| Dataset Quantization (1) | 2024.10.31 |
| Variation-aware Vision Transformer Quantization (0) | 2024.09.13 |
| Learned step size quantization (1) | 2024.09.10 |