Do We Need Zero Training Loss After Achieving Zero Training Error?

Takashi Ishida. (Tokyo Univ)

https://arxiv.org/abs/2002.08709

Do We Need Zero Training Loss After Achieving Zero Training Error?

https://github.com/takashiishida/flooding

GitHub - takashiishida/flooding: [ICML 2020] code for the flooding regularizer proposed in "Do We Need Zero Training Loss After

 

Abstract

Overparameterized deep networks는 training data를 기억할 수 있는 capacity가 있다.

일단 training data를 외우고 나면, training loss는 계속 0으로 수렴하고, test performance는 감소한다.

 

기존 정규화들은 training loss에 기준을 두지 않기 때문에, training loss를 유지하도록 하이퍼 파라미터를 튜닝하는 작업은 불가능했다.

논문에서는 training loss가 작은 값(flood value)에 도달했을 때, 더 낮아지지 않도록 조정하는 "flooding"이라는 방법을 제안했다.

 

Flooding 방법은 mini-batch gradient decent를 사용하다가, flood level 근처에 도달하면 gradient ascent를 사용하면서, flood level근처에 loss가 떠있도록 하는 것이다.

 

한 줄의 code로 간단하게 구현이 가능하고, 다른 stocastic optimizer나 regularizer와 경쟁할만한 성능을 보인다.

 

Flooding기법을 사용하면, model은 0이 아닌 training loss에서 "random walk"을 계속하며, flat 한 loss landscape로 가며 이는 일반화 성능이 더 좋아질 것을 기대한다.

 

Introduction

Generalization Gap를 두개의 stage로 나누면 다음과 같다.

1. train loss, test loss 둘 다 감소하지만, train loss가 더욱 빠른 속도로 감소
2. train loss는 감소, test loss는 증가

2번 단계에서 몇 epoch를 더 학습하게 되면, training loss는 거의 0에 가깝게 수렴한다.

만약 train data를 다 memorized한 상황이면 training loss는 0이 된다. overparameterized model일수록 overfitting이 쉽다.

 

최근 overparametrization and double descent curves 연구를 보면, training error가 0이 될 때까지 학습하는 것이 generalization error를 낮추는데 의미가 있음을 보였다. 

그러나, training error가 0이 되고 난 이후에도, training loss가 0이 될 때까지 학습하는 것이 의미가 있는 것인지는 의문이다.

 

이 논문에서는 training loss가 0가 되지 않도록 small value(flood level)에서 float 하게 하는 방법을 소개한다.

flooding 을 추가하더라도, 여전히 training data를 암기할 수 있다. training loss가 positive가 되도록 하는 것이지, flood level이 너무 크지 않는 한, training error가 positive가 되도록 하는 것을 의미하는 건 아니다.

 

Algorihm and implementation

 

기존의 learning objective를 $J$라고 할때, flooding objective를 $\tilde {J}$라고 하자. 

$\tilde {J} = |J(\theta) - b| + b$ 

 $b\, >\, 0$인 flood level이며, $\theta$는 model parameter이다.

 

$J(\theta)\,>\, b$일 때는 기존 gradient와 동일하지만, $J(\theta)\,<\,b$일 때는 기존 gradient의 반대방향을 사용한다. 

이는 mini-batch에서 동작하며, 다른 stochastic optimizer들과 경쟁할만하며, 다른 regularization 방법과 함께 사용할 수 있다.

 

Flooding 중에는 training loss가 flood level근처에서 떨어졌다, 올라갔다를 반복한다.

이는 model이 "random walk"를 하는 것인데, float loss landscape로 향하면서 더 좋은 일반화 성능을 보일 것이라고 기대한다.

 

코드로 구현하면 아래와 같이 단 한 줄로 가능하다.

outputs = model(inputs)
loss = criterion(outputs, labels)
flood = (loss-b).abs()+b  # << 요기 한줄
optimizer.zero_grad()
flood.backward()
optimizer.step()

 

 

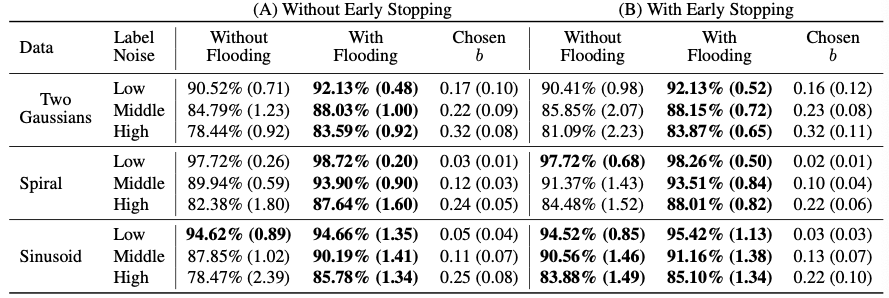
Experiments

 

ealy stopping이 성능향상에 도움이 됐고, Flooding은 early stopping과 함께 썼을때도 좋았다.

 

다양한 dataset에 대해서 실험했을때도 대부분의 경우 flooding이 성능이 높았다.