둔비의 공부공간
Rigging the Lottery: Making All Tickets Winners 본문
https://arxiv.org/abs/1911.11134
Rigging the Lottery: Making All Tickets Winners
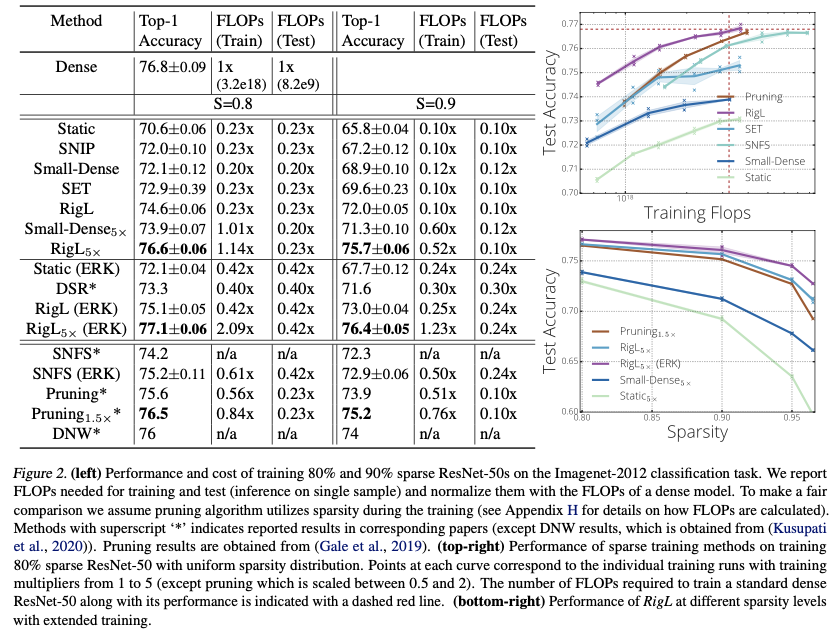
Many applications require sparse neural networks due to space or inference time restrictions. There is a large body of work on training dense networks to yield sparse networks for inference, but this limits the size of the largest trainable sparse model to
arxiv.org
2020년 ICLR paper (Utku Evci et al.)
Google Brain, DeepMind
Abstract
Training할때 정확도 손실 없이 parameter의 개수와 computational cost를 고정하여 sparse network를 학습하는 방법을 소개한다.
업데이트 할때는 주로 parameter magnitude를 사용하고, 가끔 gradient calculations를 사용한다.
이러한 방법이 더 적은 FLOPs로 이전 방법들의 accuracy에 도달 할 수 있었다.
다양한 networks와 datasets에 대해서 sparse training result SOTA를 달성했다.
최종적으로, optimization할때 topology를 변경하는 것이, topology가 static일때 local minima를 탈출하게 돕는 이유의 관점에 대해서 소개한다.
Introduction
sparse network의 paremeter와 FLOPs는 다양한 문제에서 이미 입증됐고, RNN이나 CNN에 적용하면 inference time을 빠르게 할 수 있었다.
현재 제일 정확한 sparse model을 얻는 방법은 최소 dense model을 학습하는데 필요한 memory나 FLOPs가 필요하며, 혹은 훨씬 많은 비용이 필요하기도 하다.
이러한 상황은 두가지 한계가 있다.
- sparse model의 크기는 dense model보다 클 수 없다.
- (0 or inference 할때 0이 되는) 파라미터에 대해 너무 많은 양의 계산을 해야하므로 비효율적이다.
이 논문에서는 lucky initialization없이 sparse model을 학습하는 방법을 소개한다.
그래서 "Rigging the Lottery: Making All Tickets Winners" 라고 이름을 붙였다.
Rigging The Lottery
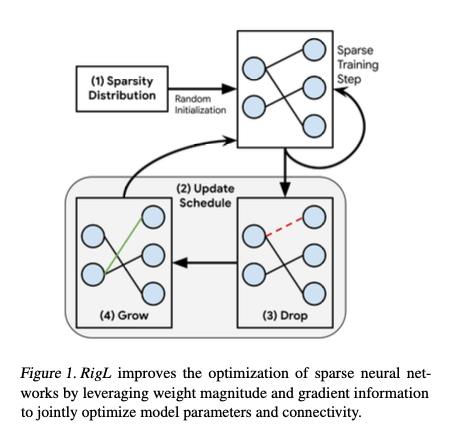

RigL은 random sparse network로 시작하고, 일정 간격으로 magnitude based로 제거하고, gradient information으로 새로운 것을 활성화한다. connectivity를 update하고 나서, 다시 학습한다.
RigL알고리즘은 크게 다음과 같이 구분할 수 있다.
- Sparsity Distribution
- Update Schedule
- Drop Criterion
- Grow Criterion
Notation
overall sparsity $S$ $=$ $\frac{\sum_{l}s^{l} N^{l}}{N}$, 전체 파라미터수중의 0의 비율로 측정한다.
Sparsity Distribution
전반적인 sparsity를 유지하면서 layer들의 non-zero weights를 분배하는 방법은 많다.
특정 FLOP budget을 맞추기 어려워지는 것을 방지하기 위해, 학습 도중에 layer간 파라미터를 재할당하지 않았다.
논문에서는 3가지 방법을 고려했다.
- Uniform
- 모든 layer의 sparsity를 전체 sparsity와 동일하게 세팅하되, 첫번째 layer는 dense하게 유지했다.
성능이 불균형해지고, total size에 큰 영향이 없기 때문이다.
- 모든 layer의 sparsity를 전체 sparsity와 동일하게 세팅하되, 첫번째 layer는 dense하게 유지했다.
- Erdos-Renyi
- 각 layer의 sparsity는 $ 1 - \frac{n^{l-1} + n^{l}}{n^{l-1} * n^{l}} $ 으로 정의한다.
이때, $n^{l}$은 layer $l$에서의 neurons의 개수이다. - 장점은, input output channel의 합에 따라서, 확장이 가능하다.
- 매개변수가 많은 곳에는 sparsity가 높게, 적은 곳에는 낮게 할당된다.
- 각 layer의 sparsity는 $ 1 - \frac{n^{l-1} + n^{l}}{n^{l-1} * n^{l}} $ 으로 정의한다.
- Erdos-Renyi-Kernel (ERK)
- 위의 식을 수정한 방법이다.
- 각 layer의 sparsity는 $ 1 - \frac{n^{l-1} + n^{l} + w^{l} + h^{l}}{n^{l-1} * n^{l} * w^{l} * h^{l}} $ 로 정의한다.
- 이게, conv의 $w,\, h$를 사용한 거라, fc의 경우 기존 공식을 사용한다.
- 위와 마찬가지로, 매개변수가 많은 곳에는 sparsity가 높게, 적은 곳에는 낮게 할당된다.
bias와 batch-norm params는 dense로 유지한다.
Update Schedule
update schedule은 파라미터 몇개를 사용한다.
- $\Delta T$ - 몇 iteration 마다 sparse connectivity를 업데이트 할 것인가?
- $T_{end}$ - 몇 iteration 까지 sparse connectivity 업데이트를 할 것인가?
- $\alpha$ - connections를 update할 초기 비율
- $f_{decay}$ - $\Delta T$ ~ $T_{end}$까지 connections를 update할 비율의 감소 함수
- cosine annealing을 사용했는데, 다른 methods의 성능을 약간 뛰어 넘었다.
- $f_{decay} (t; \, \alpha, \, T_{end}) = \frac{\alpha}{2} ( 1 + cos( \frac{t \pi }{ T_{end}} ) ) $
Drop criterion
$T_{end}$마다 connections를 제거한다.

활성화가 덜 된 weights중 상위 k%를 drop한다는 의미 인듯?
Grow criterion
논문 method의 novelty는 "How grow new connections"에 있다.
- 가장 큰 gradient를 갖고 있는 connection을 grow시킨다.
Drop criterion후에 죽은 connection중 gradient가 큰 애들은 0으로 초기화해서 살려둔다.
새로 활성화된 connections는 0으로 초기화가 되니까, network output에 영향을 주지 않는다. 하지만 다음 iteration에서 큰 gradient를 받을 것으로 기대되는 애들을 grow로 살렸으니까, loss는 더욱 빠르게 줄어들 수 있다.
활성화된 connections에 대해서 0이 아닌 다른 초기화 방법들을 써봤지만, 더 좋은 결과를 얻을 수 없었다.
이 방법은 각 layer에 순서대로 적용할 수 있고, dense gradient는 top connections를 고른 후에 바로 버릴 수 있다.
만약 full gradient가 저장하기에 너무 클땐, online 방식으로 gradient를 계산하고, 상위 k개의 gradient 값만 저장할 수 있다.
Experiments