Do We Actually Need Dense Over-Parameterization? In-Time Over-Parameterization in Sparse Training

https://arxiv.org/abs/2102.02887

Do We Actually Need Dense Over-Parameterization? In-Time Over-Parameterization in Sparse Training

(2021 ICML)

 

시작하기 전에, over-parameterization이라는 이야기가 자주 나온다.

over-parameterization이란, 우리가 필요로 하는 파라미터보다 더 많은 파라미터를 갖고 있다는 뜻이다.

그렇기에 sparse training는 과도한 파라미터를 없애고, 딱 필요로하는 파라미터만 남겨서 학습을 하면 비슷한 정확도가 나올 수 있다는 것으로 시작됐다.

 

Abstract

 

이 논문에서는 sparse training에서 ITOP("In-Time Over-Parameterization")라는 개념을 제안하여 over-parameterization 없이, SOTA급 성능을 낼 수 있는 새로운 관점을 소개한다.

 

random sparse로 초기화하고, 계속 sparse connectivities를 탐색하면서 over-parameterization 할 수 있다.

이 방법으로 sparse training과 dense training의 표현력 차이를 줄일 수 있었다.

 

ITOP를 사용하여 Dynamic sparse training의 기본 메커니즘을 이해하고, optimal sparse connectivity를 찾을 때 모든 parameter를 탐색할 수 있다는 DST의 장점을 발견했다. parameter를 충분하게 탐색한 경우, DST는 dense network보다 성능이 높아질 수 있다.

 

ImageNet에서 ResNet50으로 SOTA를 달성했는데, ITOP가 큰 sparsity에서 over-parameterization based 방법보다 더 높은 정확도를 보였다. CIFAR100에서 ResNet34로 훈련할 경우, ITOP는 98%의 sparsity에서 dense network의 성능과 일치했다.

 

 

Introduction

 

딥러닝에서는 지금까지 Over-Parameterization이 성능이 잘 나오는 것을 보여왔다.

하지만, 최근에는 sparse model도 dense model에 견줄만한 성능을 낼 수 있음을 보이고 있다.

 

대표적으로 Lottery ticket hypothesis의 경우, subnetwork를 scratch부터 학습시켜서 dense network과 비슷한 성능을 낼 수 있다는 것을 입증했지만, 이 "Winning tickets"는 fully dense over-parameterized process가 있어야 볼 수 있었다.

 

dense training에 비해 sparse traning에서는, over-parameterization 특성이 없기에, 더 낮은 표현력을 갖을 수밖에 없다.

 

위와 같은 문제를 해결하기 위한 한 가지 접근 방식은 LTH와 같은 고밀도 훈련에서 학습한 지식을 활용하는 것이다.

하지만, dense over-paramterized process를 사용하려고 하는 순간, over-parameterization dense network training 수준의 computation, memory cost가 필요하다.

 

그렇기에, 이 논문에서는 sparse tranining과 dense training의 gap차이를 줄 일 수 있는 "In Time Over-Parameterization" 개념을 제시한다.

paramter 탐색하면서 over-parameterization되는 모습

ITOP란, dense (pretrained) model의 weight대신, 학습중에 paramter를 탐색하면 over-parameterization하면서 sparse training의 expressibility를 향상시킬 수 있다는 것이다.

 

ITOP의 장점으로는 크게 4가지가 있다.

1. 높은 sparsity에서도 표현력을 높일 수 있다.
2. training, inference cost를 낮출 수 있다.
3. DST의 기본 매커니즘에 대해서 이해할 수 있다.
4. overfitting을 방지하고 일반화 성능을 향상시킬 수 있다.

위 그림 2에서 볼 수 있듯, 훨씬 적은 훈련 FLOP으로 해당 고밀도 네트워크의 성능과 일치할 수 있다.

 

 

Related Work

 

Dense Over-Parameterization

• Full dense over-parameterization
  • fully pre-trained dense model로부터 weight를 상속받는 방법으로, iterative pruning과 retaining method가 있다.
  • iterative pruning, retaining method의 3개 step으로 나눌 수 있다.
    1. dense model을 수렴할때까지 학습시킨다. (pretrained model 준비)
    2. 성능에 제일 영향을 덜 주는 weights나 neurons을 pruning한다.
       
       • Magnitude, Hessian, Mutual information, Taylor expansion
       • Variation dropout, Targeted dropout, Reinforcement learning
    3. pruned model을 재 학습하여 정확도를 올린다.
• Partial dense over-parameterization
  • dense network에서 시작해서, 학습중에 지속적으로 pruning하는 방법이다.
  • GMP(Gradual magnitude pruning)
    • target sparsity가 될때까지 점차적으로 줄이는 방법을 제안한 논문임
  • 최근에는 훈련가능한 mask를 사용하여, pruning하는 방법도 나왔다.
• One-Shot dense over-parameterization
  • 매우 최근에, initialization할때 pruning하는 방법들이 소개됐다.
    • main training 전에 trainable sparse network을 얻는 방법이다.
    • trainable sparse network를 얻으려면, 최소한 한번의 학습이 필요해서, dense over-parameterization 카테고리에 해당한다.

 

Dynamic Sparse Training

• random sparse network에서 시작해서, dynamic하게 sparse connection을 바꾼다.

 

Understanding Dynamic Sparse Training

• DST가 초기 sparse topology를 완전히 다른 topology로 최적화한다는 사실을 발견했다.
• DST는 훈련 중 gradient flow를 개선할 수 있다는 사실을 발견했다.
• 아직도 DST의 기본 메커니즘은 명확하지 않다.
  • DST가 sparse training의 성능을 향상시킬 수 있는 이유는 무엇인가?
  • DST를 통해 어떻게 sparse network가 dense network와 동등하거나 더 나은 성능을 낼 수 있는가?

 

In-Time Over-Parameterization

 

In-Time over-parameterization이란, over-parameterization없이 deep neural network를 학습시키는 방법이다.

• dense model의 over-parameterization은 parameter space의 spatial dimensionality를 말하는 것이고
• In-time over-parameterization은 space-time manifold에서 탐색되는 전반적인 dimensionality를 말한다.

 

DST를 이해하기 위해서 한가지 가설을 세운다.

DST의 장점은 optimal sparse neural network connectivity를 찾을 때, 모든 parameter를 고려할 수 있었기 때문이다.

위 가설을 3가지로 크게 나누면 다음과 같다.

1. DST는 학습도중에 parameter 탐사를 하면서, 성능이 크게 오를 수 있었다.
2. DST의 성능은 학습 도중에 안정적으로 탐색된 파라미터의 수와 밀접한 관련이 있다.
   • 안정적으로 탐색된 파라미터란, 새로 탐색된 가중치 중 pruning되지 않고, 충분히 오랫동안 업데이트된 가중치를 나타낸다.
3. 안정적으로 탐색된 파라미터가 충분하면, DST로 훈련된 sparse network는 높은 sparsity에서도 dense network와 일치하거나 더 좋은 성능을 발휘할 수 있다.

 

방법은 간단하다.

 

일단, dense network를 학습하고 ($\theta$), sparsity network를 만들어서 학습한다 ($\theta_{sparse}$).

이때, 일정 iteration마다 sparse connectivity를 업데이트해준다. 이 iteration마다 얻은 weight를 $\theta_{sparse}^{i}$라고 할때

In-Time Over-Parameterization rate ($R_{s}$)는 (0이 아닌 sparse connectivity weights의 개수의 합 / 0이 아닌 dense network weight의 개수의 합)으로 구할 수 있다.

 

iteration주기를 짧게 가져갈 수록, 더 많은 parameter를 탐색할 수 있을 것이고, 그러면 가설에 따라서 test accuracy는 오를 것이다.

그러나, reliable exploration threshold보다 낮아지는 순간, test accuracy는 감소할 것이다.

• 새로운 weight는 충분한 update를 받지 못하여 안정화되지 못했기 때문이다.

 

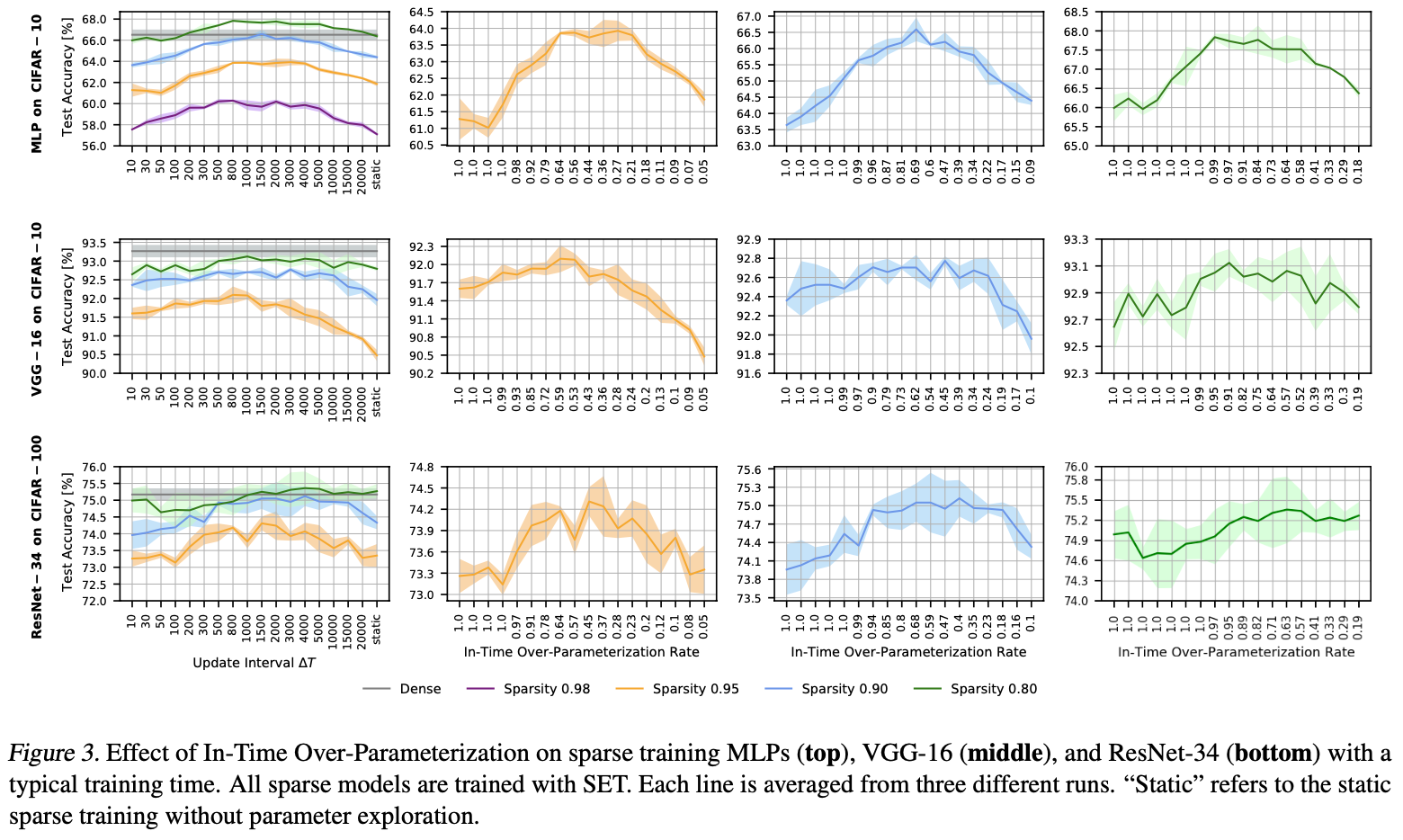
그림3을 보면, In-Time Over-Parameterization Rate에서 모든 parameter에 대해서 탐색했음에도 불구하고, 안정적이지 못한 parameter로 인해 test accuracy가 낮아지는 것으로 보인다.

 

그림4를 보면, 지속적으로 parameter exploration을 하지 않은 (노란 점선)의 경우, 낮은 accuracy를 달성한 것을 볼 수 있다.

그러나, 모든 모델들은 epoch와 $R_{s}$가 늘어가면 정확도가 올라가는 것을 볼 수 있다.

즉, 시간적으로 parameter space를 안정적으로 탐색하면 sparse network의 expressibility가 계속 향상된다.

• 낮은 sparsity는 시간적으로 안정적으로 탐색할때까지 필요한 시간이 적다.
• 또한, 시간이 지날수록 overfitting으로 인해 정확도가 낮아지는 dense모델과 다르게, sparse model의 경우, $R_{s}$가 늘어나는동안에는 accuracy가 계속 오르는 것을 볼 수 있다.

 

Effect of Weight Growth methods on ITOP

 

 

gradient based weight growth (RigL and SNFS)의 경우, iteration주기가 감소하면, acc가 올랐다가 내렸다가 다시 오르는 것을 볼 수 있다. random based growth(SET)와 비교했을때, gradient based (RigL)는 안정적인 parameter exploration에서 더 큰 이득을 얻고, 불안정한 parameter exploration에서 더 큰 손해를 본다.

 

이는 RigL의 경우, high gradient magnitude로 new weight를 성장시키기 때문인데, 이는 exploration에서 더욱 빠르게 loss를 감소시킬 수 있지만, 기울기가 큰 weight는 결국 크기가 커져 pruning threshold가 커질 가능성이 높으므로 안정적인 탐색을 보장하려면 iteration을 더 높게 설정해야한다.

 

RigL에서 iteration주기를 4000으로 설정했을때, $R_{s}$가 증가함에 따라서, 성능이 오르는 것을 볼 수 있었다.

특정한 학습까지는 RigL이 SET보다 성능이 높았으나, 충분한 학습을 하고 난 이후에는 SET의 성능이 더 높아졌다.

RigL이 SET보다 $R_{s}$가 낮은데, 이는 gradient weight가 성장하면서, sparse connectivity를 특정 유사한 structure로 보내고, 표현력을 제한하는 결과를 가져온다는 것을 나타낸다.

 

반대로, random growth는 paramter를 탐색하기 위해 전체 search space를 고려하며, local optima를 더 잘 찾을 수 있게 된다.

하지만, 이러한 결과는 큰 데이터셋에서 large-scale architecture를 사용했을때와는 다르다.

 

RigL은 ImageNet과 Resnet50에서 SET보다 더 높은 성능을 보였으며, 이러한 결과는 각 sparse connectivity를 갱신할때, dense gradient가 제일 좋은 weight를 찾게 도와주기 때문이다.

large-scale architecture에서 SET는 이러한 좋은 weight를 찾는데, 더 많은 시간을 필요로 한다. (sparsity가 크면 클수록 오래걸린다.)

 

Effect of Batch Size on ITOP

 

또한, 제한된 시간내에 DST의 성능을 올릴 수 있는 방법을 발견했는데, small batch size로 학습하는 것이다.

small batch size로 학습하는 것은 더 많은 update를 가능하게 하고, 이는 $R_{s}$의 증가로 이어지게 된다.

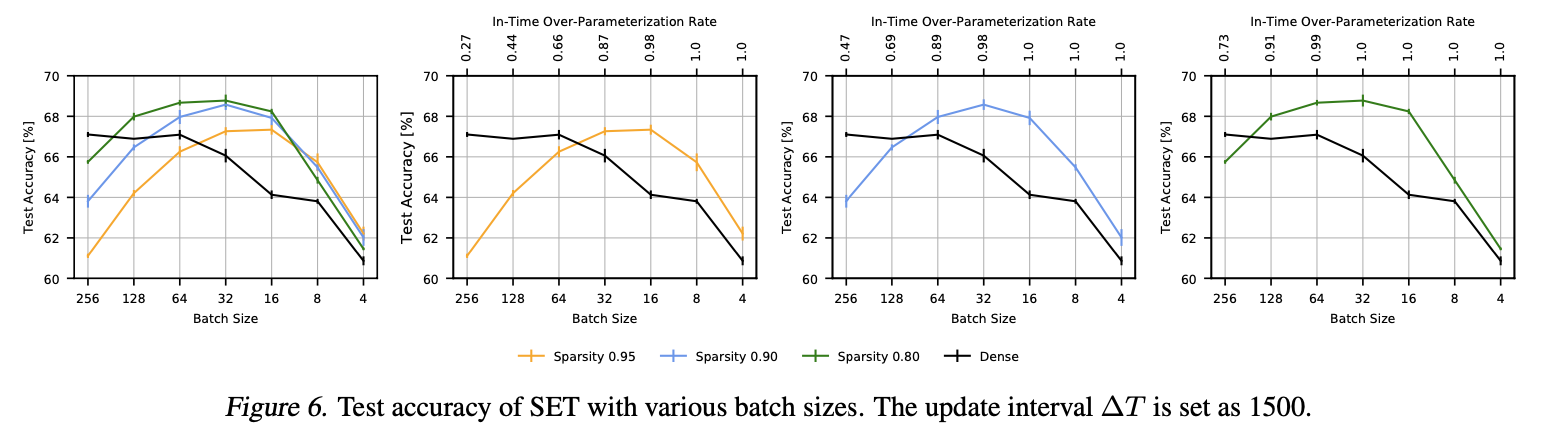
그림6을 보면, batch size가 감소함에 따라 $R_{s}$와 acc가 같이 증가하는 것을 볼 수 있다.

물론, 특정 batch size이하로 내려가게 되면, SGD의 "noise scale"이 증가하면서 정확도가 큰 폭으로 감소한다.

 

Effect of Pruning Rate on ITOP

 

상대적으로 큰 pruning rate는 넓은 범위의 parameter탐사를 하게 하면서, 더 높은 정확도를 달성할 수 있지만

과도하게 큰 pruning rate는 모델 자체의 capacity가 낮아지면서, 성능이 나오지 않게 된다.

 

Boosting the Performance of DST

 

위에서 언급했던 모든 것을 활용해서 ImageNet + ResNet50의 성능을 측정해보았고 SOTA를 달성했음을 확인했다.

 

Iteration 4000, batch size 64, pruning rate 0.5를 사용해서 높은 $R_{s}$를 달성할 수 있었다.

작은 batch size대신 parameter exploration을 하는 방법으로 선택한건, new weight를 성장시킬때, 활성화되지 않은 weight에서 먼저 sampling하여 성장시키는 방법이다.

활성화 안된 weight를 먼저 활성화시키는 방법인 SET+

 

Conclusion and Future Work

 

이 논문에서는 "ITOP"를 제안했다.

• 시공간적 manifold에서의 dense over-parameterization의 변형임
• dense over-parameterized dependency없이 network를 학습할 수 있게 됐다.

 

ITOP의 장점은 다음과 같다.

• sparse training에서 표현력을 향상시킬 수 있다.
• training과 inference를 빠르게 할 수 있다.
• DST의 매커니즘에 대해서 이해할 수 있다.
• overfitting을 방지하고, 일반화 성능을 향상시킬 수 있다.

일반화 성능 비교

 

또한, 충분히 안정적인 파라미터를 탐색하고 나서는 randomly-initialized sparse model이 특정 initialized static sparse model보다 성능이 높은 것을 확인했다.

즉, 모든 파라미터로 좋은 sparse initialization을 찾는 것보다, 특정 파라미터들로 여러번 탐색하는 것이 더 좋고 효율적이다.