DYNAMIC SPARSE TRAINING: FIND EFFICIENT SPARSE NETWORK FROM SCRATCH WITH TRAINABLE MASKED LAYERS

https://arxiv.org/abs/2005.06870

Dynamic Sparse Training: Find Efficient Sparse Network From Scratch With Trainable Masked Layers

(ICLR2020)

 

Abstract

DST : 학습가능한 pruning thresholds로 optimzation하면서, optimal parameter + sparse network를 함께 찾는 방법

• 이 pruning thresholds는 backpropagation을 통해서 layer별로 학습된다.

아주 약간의 performance loss가 있지만, dense network와 동일한 epoch로 쉽게 sparse network를 학습시킬 수 있다.

다른 sparse training algorithms과 비교했을때 SOTA를 달성했다.

 

왜 DST가 효율적이고 효과적인지에 대한 증거도 제시하면서, 기존 3-stage algorithms (dense, prune, retrain)의 문제점도 밝혔다.

 

Introduction

기존 pruning방법들은 dense network training -> pruning -> fine-tuning iteration으로 구성됐다.

이 pruning and fine-tuning iterations의 cost를 줄이기 위해서, training과정에서 pruning하는 방법들이 제시됐지만, 문제가 있었다.

1. Coarse-grained predefined pruning schedule.
   • pruning ratio, finetuning epoch, total pruning step등 모델마다 다양하게 설정해야했고, 설정에 따라서 너무 다양한 모델이 나왔다.
2. Failure to properly recover the pruned weights.
   • 기존 pruning methods들은 "hard" pruning으로 구성됐다. (set weight to 0)
   • 또 많은 연구에서는 dynamic하게 weight가 변하는게 중요하다고 했다. (필요 없던 weight가 중요해지는 경우도 있다.)
   • 하지만, hard pruning에 경우 parameter 중요도의 정보가 아예 날아가게 되며, 아래와 같은 문제가 생긴다.
     • pruning된 weight를 살려야할까?
     • 살린다면 어떤 값으로 살려야할까?
   • 위와 같은 문제로 weight를 살릴때, pruning된 애들중 $p%$비율을 미리 정한 값으로 살리거나, 랜덤 초기화하는 방법을 사용했다.
3. Failure to properly determine layer-wise pruning rates.
   1. 최신 신경망들은 여러 layer를 갖고, layer마다 다양한 parameters를 갖기 때문에, layer마다 필요없는 파라미터의 수는 다 다르다. 그러므로, 동일한 값으로 pruning을 해서는 절대 optimal하지 않는다.
   2. layer-by-layer greedy pruning methods의 문제점은 초반에 불필요한 neurons가 나중에 상당히 중요해질수도 있다는 점이다.

그렇기에 논문에서는 위의 문제를 해결한 end-to-end sparse training algorithms를 제안한다.

 

논문에서 제안한 방법에 대한 장점은 다음과 같다.

1. Step-wise pruning and recovery
   1. 각 training step에서 prune & recover한다.
   2. 기존 방법에서는 epoch사이에 넣는 방법이 많았는데, step단위로 진행하므로 더 자주 세분화하여 pruning할 수 있다.
2. Neuron-wise or filter-wise trainable threshold
   1. 기존 방법들은 각 layer 혹은 전체 architecture마다 하나의 pruning threshold를 사용했었다.
   2. 논문에서는 각 layer마다 threshold vector를 사용해서 fc, rnn에 대해서 neuron-wise pruning threshold를 갖을 수 있고 cnn에 대해서는 filter-wise pruning threshold를 갖을 수 있다.
   3. 또한, threshold vector는 고정된 값이 아니라, 학습이 가능하므로 back-propgation과정에서 자동적으로 update된다.
3. Dynamic pruning schedule
   1. 논문의 방법은 schedular로 인해 변하는 lr에 따라,  layer-wise pruning rate가 변경될 수 있다.
4. Consistent sparse pattern
   1. 논문의 방법은 다른 model sparsity에서도 안정된 payer-wise sparse pattern을 얻을 수 있다.
   2. (sparsity에 따라서, optimal layer-wise pruning rate를 자동적으로 구할 수 있기 때문이다.)

 

Related Work

Sparse Neural Network Training

• Sparse Evolutionary Training (SET)
  • pruning된 neurons와 connection이 랜덤으로 살아나는 방법.
  • sparsity level은 사람이 정해야하고, 랜덤으로 살아났을때의 network변화는 예측이 불가능했다.
• DEEP-R
  • pruning과 regrowth를 Bayesian sampling으로 결정하는 방법.
  • 계산 비용이 너무 비쌌다.
• Dynamic Sparse Reparameterization
  • sparse structure를 찾기 위해, dynamic parameter reallocation을 사용하는 방법.
  • pruning된 paramter 비율이 높을때는 pruning threshold가 절반이 되고,
    특정 layer에 대해 pruning된 paramter 비율이 낮을때는 pruning threshold가 두배가 되는 방법으로만 구할 수 있었다.
  • 그렇기에 threshold를 coarse-grained하게 얻는 방법은 Dynamic Sparse Reparameterization에 좋지 않았다.
  • 심지어, pruning ratio, fractional tolerance가 필요했다.
• Dynamic Network Surgery
  • parameter magnitude에 따라서 pruning or recover하는 방법
  • 하지만, threshold를 선택하고, sparse learning process동안 그 값을 사용한다.
  • 이러한 layer-wise threshold는 정하기 정말 힘들고, 고정된 threshold는 parameter 중요도를 빠르게 바꾸기 힘들다.
• Sparse networks from scratch
  • exponentially smoothed gradients를 pruning and regrowth의 기준으로 사용하는 sparse momentum을 제안함.
  • 미리 정해둔 비율만큼 각 pruning step에서 pruning하는데, pruning, momentum scaling rate 상대적으로 높은 parameter space에서 찾아야한다.

 

Dynamic Sparse Training

시작하기 전 잠깐의 Notation

• $W_{i}$ : $i$번째 layer의 parameter matrix
• $C$ : network layer의 개수
• $c_{i}$ : input dimension
• $c_{o}$ : output dimension
• $K_{i}$ : i번째 layer의 kernel로 $c_{0} \times c_{i} \times w \times h$의 dimension을 갖는다.
• $M_{i}$ : $i$ layer의 binary pruning mask
• $\odot$ : Hadamard product operator

Threshold Vector and Dynamic parameter mask

논문의 목적은 $\{W_{1}, W_{2}, W_{3}, ... ,W_{C}\}$가 주어졌을때, $\{M_{1}, M_{2}, M_{3}, ... ,M_{C}\}$ 을 dynamic하게 찾는것이다.

 

이를 위해서, 각 $W$에 대해 학습가능한 pruning threshold vector $t$를 정의한다.

또한, step function $S(x)$를 정의하여, paramter magnitude와 해당 threshold에 따라 mask를 구한다.

여러 step size function $S(x)$와 $S(x)$의 미분값을 근사한 함수들

$|W_{ij}|$에 threshold $t_{i}$를 뺀 값에 unit step function $S(x)$를 거쳐서 mask $M_{ij}$를 만든다.

$W_{ij}$에서 pruning이 필요하다고 판단되면, $M_{ij}$에 해당하는 값이 0으로 세팅된다.

이때, $W_{ij}$값 자체는 지우지 않고 파라미터 중요도에 대한 historical 정보로 남겨둔다.

 

fc나 recurrent layer의 경우, $W_{ij}$는 뉴런별 threshold $t_{i}$를 갖고, $W_{ij}$는 {i}번째 출력 뉴런과 관련된 {j}번째 weight다.

cnn의 filter-wise threshold의 경우, matrix or single scalar threshold를 사용한다.

 

Trainable masked layers

fc나 recurrent layer에서 dense paramter $W$ 대신, sparse product $W \odot M$ 이 사용된다.

cnn에서 convolution kernel $K$ 를 flatten해서 $W$ 로 만들면, kc나 recurrent layer처럼 적용할 수 있다.

이 sparse kernel은 conv연산 뒤에 사용된다.

 

기존 step function $S(x)$는 back-propagation에 사용할 수 없어서 (그림2의 c), (그림2의 d)같은 approximate function들이 등장했다.

• 미분하면 모든곳에서 gradient가 0가 되면서, back-propagation을 할 수 없다.

논문에서는 $S(x)$를 미분하는 것 대신, 미분한 형태와 비슷한 $H(x)$를 사용했다.

그림 2(d)에서 볼 수 있듯, 이 방법은 훈련 중 gradient vanishing을 방지하기 위해 gradient가 0이 아닌 [-1, 1] 범위를 갖는다.

반면에 0에 가까운 기울기 값은 부분 다항식 함수로 STE보다 더 정밀한 근사치를 제공한다.

long-tailed estimator $H(x)$

이 $H(x)$를 사용하면서, vector threshold $t$는 back-propagation으로 학습할 수 있다.

trainable masked layer에서 network parameter $W$는 performance gradient와 sparse gradient로 학습하게 된다.

 

그러므로, pruned weight, unpruned weight, threshold vector는 각 training step마다 back-propagation을 통해 학습할 수 있게 된다. 

 

Sparse Regularization Term

high sparsity masks $M$을 얻기 위해, 높은 pruning threshold가 필요하다.

 

sparse regularization term $L_{s}$를 도입하여 low threshold value에 대한 패널티항을 추가했다.

$R_{i} = \sum_{i=1}^{c_{o}} exp(-t_{i})$

$L_{s}\,=\, \sum_{i=1}^{C} R_{i}$ 

 

$exp(-x)$ 함수이므로, $t$값이 커질수록 0에 수렴하는 형태다. $t$값을 커지게 만들어, high sparse mask $m$을 얻을 수 있다.

 

Dynamic Sparse Training

최적화 함수

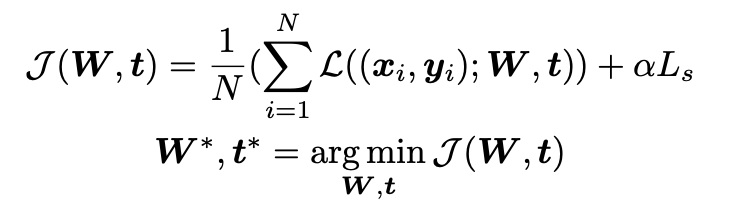
fc, convm, recurrent layers는 trainable masked layers와 함께 사용할 수 있다.

$W$, $t$는 $loss$를 최소로 하는 방법으로 optimize가 된다.

 

$\alpha$는 regularization term을 조절하는데, $L_{s}$에서 $t$가 커지면 sparse해지고, performance loss는 낮아진다.

그러므로 dynamic하게 적절한 performance와 sparsity의 balance를 맞춰가며 학습한다.

 

Experiments

MNIST, CIFAR10, ImageNet에 대해서 실험을 진행했다. 

모델은 fc, conv, rnn을 사용했다.

 

layer별 remaining ratio는 $k_{l} = n / m$가 된다. (0이 아닌 mask의 비율)

$n$ : number of elements equal to 1 in mask $M$

$m$ : total number of element in $M$

 

모든 trainable masked layers에 대해서, trainable thresholdsms 0으로 초기화하여, dense network와 동일하게 설정했다.

 

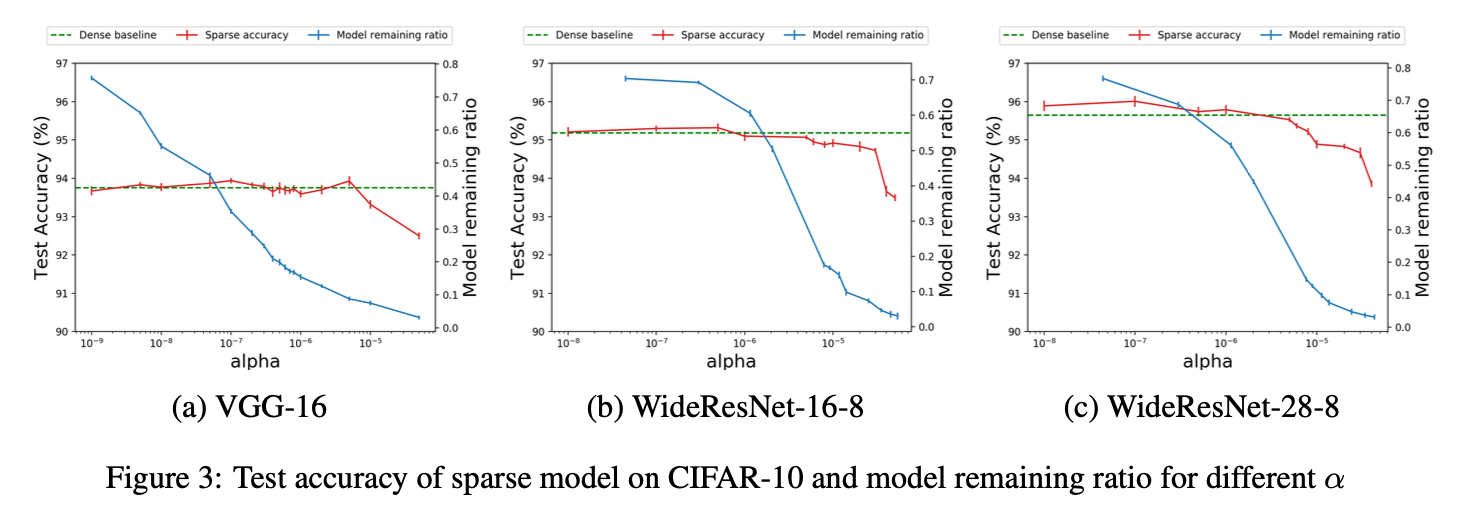
Pruning performance on various datasets

MNIST

CIFAR10

ImageNet

 

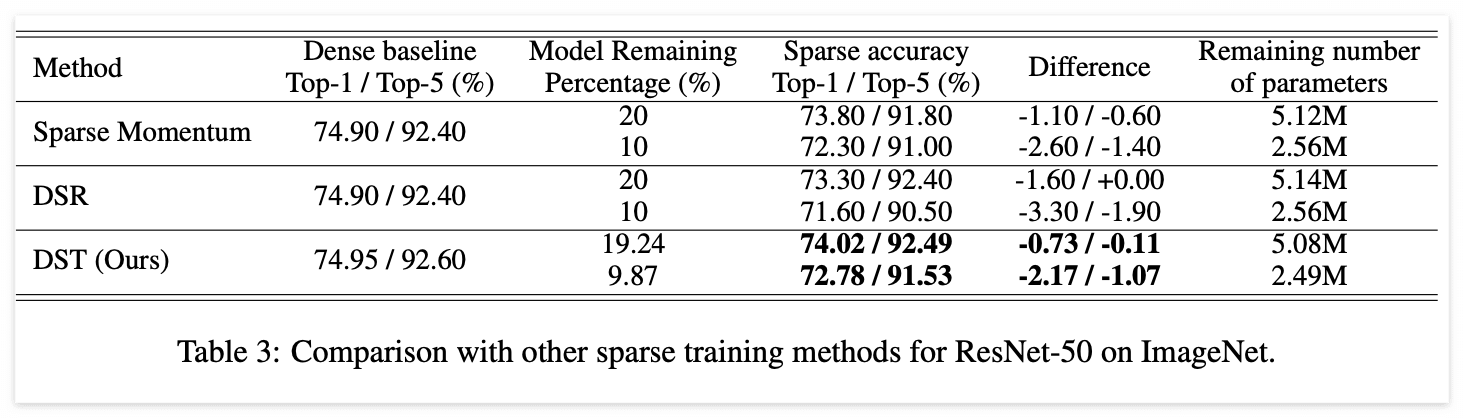
Pruning performance on various remaining ratio

$alpha$가 커질수록 pruning이 많이 되고, test acc는 하락하는 모습