둔비의 공부공간
Scale Decoupled Distillation 본문
https://arxiv.org/abs/2403.13512
Scale Decoupled Distillation
Logit knowledge distillation attracts increasing attention due to its practicality in recent studies. However, it often suffers inferior performance compared to the feature knowledge distillation. In this paper, we argue that existing logit-based methods m
arxiv.org
Abstract
기존 logits distillation 방법은 sub-optimal한 문제가 있다고 주장한다.
- 다양한 semantic knowledge에 대해서 global logit output만을 사용하기 때문이다.
- 이는 student 입장에서는 모호한 지식 증류가 되며, mislead로 이어지게 된다고 주장한다.
이러한 문제를 해결하기 위해서 Scale Decoupled Distillation (SDD)를 제안했다.
- global logit output을 multiple local logit output으로 나누고 distillation을 한다.
decoupled knowledge는 consistent(semantic information)와 complementary logit knowledge(sample ambiguity)로 나눌 수 있다.
complementary logits에 파라미터를 키우면 모호한 sample에 대해서 student가 더 집중할 수 있도록 해준다.
Method
image input $x$
teacher $T$
student $S$
network를 두가지로 쪼갰다.
- conv feature extractor $f_{Net}$, Net = {T, S}
- feature map as $f_{Net}(x)$ in $c_{Net} x h_{Net} x w_{Net}$
- projection matrix $W_{Net}$ in $c_{Net} x K$
- f_{Net}(x)에서 뽑은 feature vector를 $K$ class logits $z_{Net}^{l}$ (l=1~K) 으로 projection 시킨 것
- f_{Net}(j, k) = f_{Net}(x)(:, j, k) in $c_{Net} x 1 x 1 $
- j, k의 위치에 있는 feature Cx1x1 이라는 뜻
- 이는 receptive field theory에 따라서, f_{Net}(j, k)는 ($t_{x}$, $t_{y}$, $t_{x}+d$, $t_{y}+d$) in $x$ 와 같다.
- $t_{x} = d * j$, $t_{y} = d * k$. $d$는 input과 final feature map간의 downsampling factor다

그니까 모든 feature를 다 더해서 평균내는거니까 avgpooling이고 이 값을 weight에 곱해준 게 들어간다.
Scale Decoupled KD

SDD는 두가지를 고려한다.
- Multi-scale pooling
- feature map이 주어지면, 다 다른 scaling로 avg pooling을 진행한다.
- information weighting
- 최종적으로, information weighting은 global logits과 local logits이 일치하지 않는 모호한 샘플에 대해 더 많은 관심을 갖도록 안내하는 역할을 한다.
$C(m,n)$을 $n$번째 cell에 $m$번째 scale이라고 가정하자
$Z(m, n)$은 이 cell에 해당하는 input region이라고 할때, $\pi_{T}(m,n)$ in Kx1x1이다.
이 logits은 teacher의 $Z(m,n)$ input region에 해당하는 logits이 된다.

m은 {1, 2, 4, ..., w}이고, 대응되는 cells은 $N_{m}$ = {1, 4, 16, ..., w^2}이다.
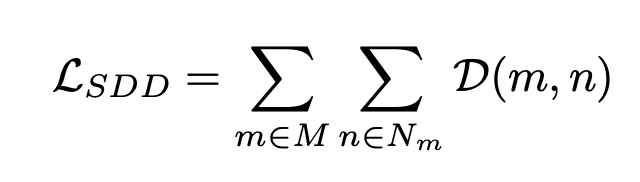
여기서 scaled로 분리된 logits output을 class 결과에 따라서 두개로 나눈다.
- global logits 출력과 동일한 class에 해당하는 항목들
- global logits 출력과 다른 클래스에 속하는 보완적인 항목들
첫번째는 다중 스케일 지식을 전달하고, 두번째는 샘플의 모호성을 보존해준다.
또한, 전역 예측이 맞고 로컬이 틀렸을때는, 일관되지 않은 로컬지식이 샘플의 모호성을 보존하도록 하며 과적합을 피하게 해준다.
반면에, 전역 예측이 잘못되었을때 로컬 예측이 올바른 경우, 일관되지 않은 로컬지식은 학생이 서로 다른 category간의 유사한 구성요소에서 배우도록 하며, 교사에 의해 유발된 편향을 완화시킬 수 있다.

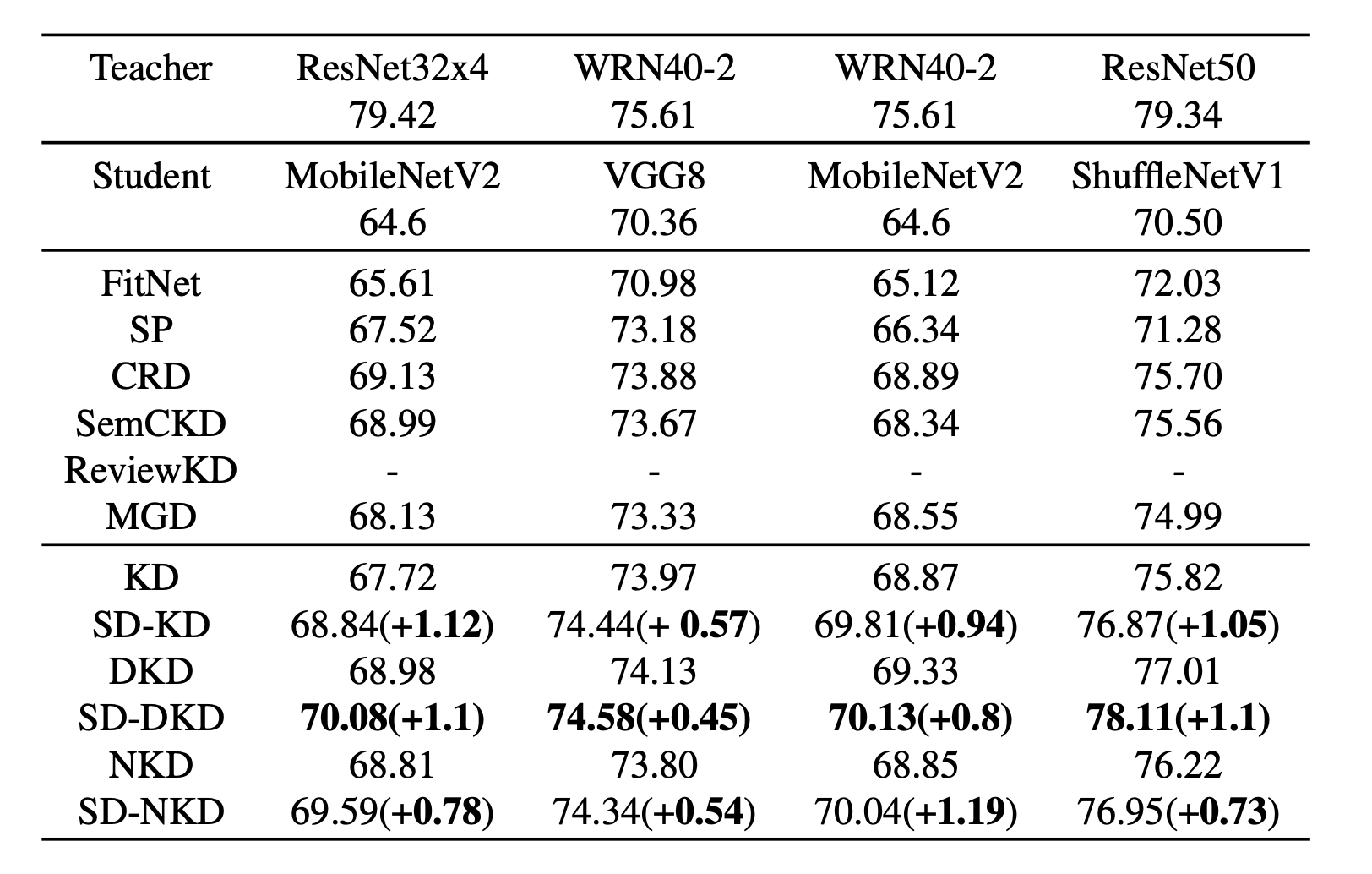
동일한 아키텍쳐에선 M {1, 2}를 다른 아키텍쳐에서는 M{1, 2, 4}를 사용했다.
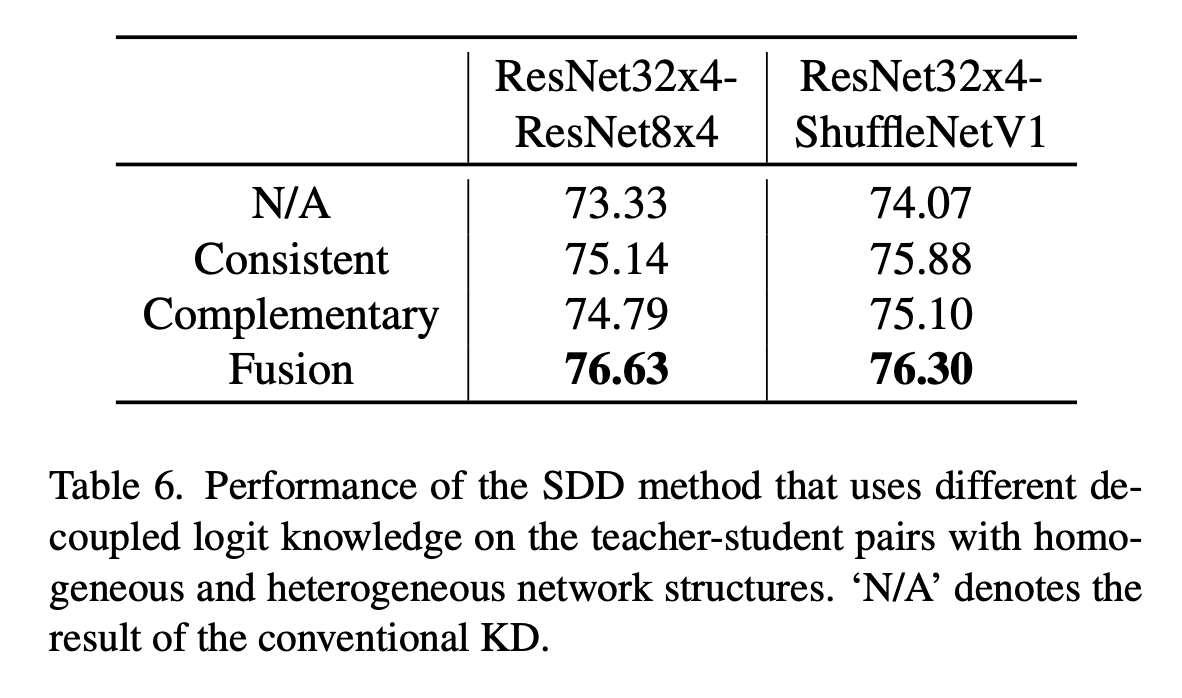
내가 하던거랑 너무 비슷한게 나와버렸다.. ㅠㅠ




