둔비의 공부공간
Fantastic Weights and How to Find Them: Where to Prune in Dynamic Sparse Training 본문
Fantastic Weights and How to Find Them: Where to Prune in Dynamic Sparse Training
Doonby 2024. 6. 7. 13:10https://github.com/alooow/fantastic_weights_paper
GitHub - alooow/fantastic_weights_paper: Repository for the paper: "Fantastic Weights and How to Find Them: Where to Prune in Dy
Repository for the paper: "Fantastic Weights and How to Find Them: Where to Prune in Dynamic Sparse Training" - alooow/fantastic_weights_paper
github.com
NeurIPS 2023 Accepted
Abstract
Dynamic Sparse Training은 학습과정에서 adapting하면서 network의 sparse initialization을 최적화하는 분야이다.
특정 조건에서 DST는 Dense의 성능도 이길 수 있다고 한다.
이 DST framework에서 제일 중요한건 "pruning" and "growing" criteria이다.
"growning"이 DST performance에 끼치는 영향은 많이 연구가 된 반면에, "pruning"의 영향은 많이 연구되지 않았다.
이 논문에서는 "pruning" 기준을 실험적으로 분석하고 적용하여 DST dynamic에 미치는 영향을 더욱 잘 이해할 수 있었다.
놀랍게도 대부분의 연구들이 비슷한 결과를 보이는 것을 확인했으며, magnitude-based pruning이 제일 성능이 좋았다.
Introduction
최근[15]에서는 iterative pruning에 parameter re-initialization을 결합하여 dense 모델과 유사한 성능을 달성할 수 있는 sub-network를 찾을 수 있음을 발견했다.
이러한 결과는 "lottery ticket hypothesis"라고 부르며, initialization부터 이미 sub-network를 찾고 훈련하는 수많은 후속 논문들이 나왔다.
또한, Dynamic Sparse Training framework는 뇌의 신경 재생에서 영감을 받아 모델의 일부 parameter를 반복적으로 pruning하고 re-growing하는 과정을 통해, network의 초기 sparse connectivity의 유연성을 확보한다.
- (20%의 parameter만 갖고 ResNet50에서 ImageNet을 학습한 모델의 성능 저하가 없었다고 한다.)
강화학습 분야에서는 dense보다 성능이 뛰어난 경우도 있었고, adversarial robustness 측면에서는 sparse network구조를 찾아 학습한 모델이 dense보다 robust하다는 결과도 있었다.
기존까지의 DST연구들은 "growing"에 초점을 맞추고 연구를 진행했지만, 이 논문에서는 complementary approach를 택하여 pruning 방법에 중점을 두었다.
DST의 pruning 기준은 weight의 importance를 측정하고, 이를 특정 connection의 "유용성"으로 사용한다. connection importance의 경우, network의 plasticity와 adaptation으로, 훈련 과정에서 변화될 수 있다. 이러한 이유로 DST는 학습이 끝난 이후에 진행하는 pruning과는 다르다.
- (현재 중요하지 않은 weight가 학습 후반에는 중요할 수도 있다는 뜻.)
이 논문의 목표는 pruning criterion과 DST의 동적 변화 관계를 더 잘 이해하는 것이다.
이를 위해서, 저자들은 여러 연구를 수행하고 다양한 모델에서 DST framework에 미치는 영향을 분석했다.
논문이 발견한 내용은 다음과 같다.
1. 안정적인 하이퍼파라미터에서 진행된 DST는 모델구조나 growth criterion과 무관하게 비슷하게 동작했다.
2. 매우 sparse한 상황에서는 성능차이가 크게 발생한다. (magnitude가 제일 좋더라)
3. 몇 번의 connectivity update만으로도 좋은 결과를 달성할 수 있다.
4. 각 criterion에 대해 pruning된 집합들의 구조적인 유사도를 분석해보니, 좋은 성능을 내는 방법들이 비슷한 결정을 내리는 것을 확인했다.
이 연구는 상당히 많은 pruning 방법이 많음에도 불구하고, 여전히 magnitude 기반의 pruning이 좋다는 것을 보였다.
Pruning Criteria
pruning fraction $p_{t}$가 주어지면, pruning criterion $C$는 각 weight에 대한 importance score $s(\theta^{l}_{i,j})$를 계산하고, 작은 값의 weight를 pruning한다. (논문에서는 편의를 위해서 layer 구분없이 $\theta$ 라고 표기했다.
논문에서는 local pruning을 사용했다.
- local pruning
- 50% 프루닝을 진행한다면, 각 layer별로 50%의 weight를 pruning한다.
- (모든 layer의 pruning ratio는 50%로 동일하다.)
- global pruning
- 50%의 프루닝을 진행한다면, 전체 layer의 weight에 대해서 50%를 pruning한다.
- (특정 layer의 pruning ratio는 50%보다 클수도, 작을수도 있다.)
- 최초로 DST framework에서 사용된 pruning criterion이다.
- 절대값이 가장 작은 positive and negative weights를 동일한 양만큼 pruning한다.
Magnitude
- 절대값이 가장 작은 weight를 pruning한다. SET와 다른점은 positive 와 negative를 동일한 양만큼 pruning하지 않는다는 것이다.
- magnitude의 심플함과 효율성으로 인해, standard post-training pruning[Link1][Link2]에서 많이 사용되고 있다.
- 기존 Magnitude는 학습중에 weight의 변화에 대해서는 고려되지 않는다는 문제가 있었다. MEST는 gradient를 weight's의 magnitude trend의 척도로 사용한다.
- $s(\theta)$ = $|\theta| + \lambda|\triangledown_\theta \mathcal{L}(\mathcal{D})|$
- MEST처럼 gradient의 정보를 pruning의 criterion으로 활용하려고 한 다른 논문이다.
- control system에서 영감을 받아서, weight의 절대값과 gradient의 상대적 크기에 대한 criterion을 제안했다.
- $s(\theta)$ = $|\triangledown_\theta \mathcal{L}(\mathcal{D})| / |\theta|$
- 이 논문의 저자들은 Sensitivity에 역수를 취한 버전이 좀 더 안정적임을 발견했다.
- Rsensitivity, $s(\theta)$ = $|\theta|/|\triangledown_{\theta}\mathcal{L}(\mathcal{D})|$
SNIP
- weight를 지우기 전과 후의 loss의 차이에 대한 First-order Taylor approximation를 기반으로 만든 criterion이다.
- $s(\theta)$ = $|\theta| * |\triangledown_\theta \mathcal{L}(\mathcal{D})|$
- 이는 static sparse training과 post-training pruning에서 이미 잘 사용하던 방법이다.
- 논문의 저자들은 DST scenario에서의 성능을 조사했다.

Methodology
이 논문에서는 아래 질문에 답하며, DST pruning 방법간의 차이점과 유사점을 분석한다.
Q1: 다양한 pruning criterion이 DST 성능에 미치는 영향은 무엇인가?
Q2: topology update frequency가 다양한 pruning 효과에 어떻게 영향을 미치는가?
Q3: 다양한 pruning criterion이 유사한 network topologies를 생성하는 정도는 어느 정도인가?
Q1: 다양한 pruning criterion이 DST 성능에 미치는 영향은 무엇인가?
위 질문에 대답하기 위해, 논문의 저자들은 pruning criterion과 network의 최종 성능 사이의 관계를 조사했다.
다양한 아키텍쳐(<100K ~13M parameter) 와 데이터셋에서 다양한 pruning criterion 결과를 비교했다.
growing criterion은 uniform random[Link]과 gradient[Link] 방법을 사용했다.
예상하기로는, weight의 magnitude와 gradient 정보를 결합한 방법이, weight magnitude에만 의존하는 것보다 더 좋은 성능을 보일 것이다. gradient는 가중치의 미래에 대한 정보를 제공할 수 있기 때문에, connectivity가 지속적으로 바뀌는 DST에서는 미래 update에 대한 정보가 유익할 수 있다.
Q2: topology update frequency가 다양한 pruning 효과에 어떻게 영향을 미치는가?
위 질문의 답하기 위해, 논문의 저자들은 topology update period $\delta t$에 중점을 두었다. (network의 구조가 바뀌는 주기이다) 이 파라미터는 mask가 바뀌기 전, network가 훈련할때 보는 data의 샘플수와 연관이 있다. 그러므로 상대적으로 낮은 값을 사용하게 된다면, 최적화가 되기 전에 topology가 자주 변경되어 connection이 완전한 잠재력을 갖지 못할 위험이 있다고 이야기한다. 반면에, 높은 값을 사용하게 된다면 network의 구조가 바뀌지 않는 문제가 발생한다. 이러한 문제점을 이야기하며, exploitation exploration사이에서 균형을 찾는 것이 DST에서 중요한 과제라고 저자들은 이야기한다.
Q3: 다양한 pruning criterion이 유사한 network topologies를 생성하는 정도는 어느 정도인가?
Q1과 Q2에서는 pruning criterion이 DST에 미치는 요소 (성능, update freq)를 설명했고, Q3에서는 과연 mask solution이 다르게 구성되는가? 에 대한 것을 분석하려고 한다.
학습이 끝난 후 얻은 최종 mask의 유사성과 sparse initialization과 얼마나 가까운지를 조사하여 DST topology update가 mask구조를 변화시키는데 의미가 있는지를 판별한다.
이를 위해서 두 집합의 근접성을 평가하는 Jaccard index(or Intersection-Over-Union)을 사용하여 layer에 대해서 별도로 계산하고 평균내어 계산했다고 한다.

$\mathcal{I}_{a}^ {l}$과 $\mathcal{I}_{b}^ {l}$는 layer $l$에서 pruning criteria a와 b로 선택된 집합들이다.
결과값 1은 완벽하게 겹치는 것이고, 0은 전체가 분리되어있다는 것을 암시한다.
Experiments
$\delta t$ = 800, initial pruning fraction $p=0.5$ + cosine decay
random and gradient based growth criterion approches.
ResNet50은 density 0.2 + gradient based growth을 사용했다.
다양한 pruning criterion이 DST 성능에 미치는 영향은 무엇인가?

DST framework에서 pruning criteria가 test accuracy에 미치는 영향을 분석했다.
dense와 static with ERK initialization과 비교하였으며, 그 결과는 위 그림1과 같다.
다양한 pruning criteria간의 차이는 낮은 density (높은 pruning ratio)에서 크게 나타났으며, DST framework는 대부분 static pruning방법보다 항상 좋았다.
분석해보면, Sensitivity와 SET, MEST방법이 항상 Magnitude보다 좋지는 않았으며, 오히려 비슷하거나 낮은 경우가 많았다고 한다.
RSensitivity는 다른 방법보다는 더 나은 성능을 보였지만, 높은 density (낮은 pruning ratio)에 적합하다고 한다.

특정 상황에서 DST가 dense보다 더 좋은 결과를 얻을 수 있다는 것을 보였으며, 이는 새로운 연결을 제거하고 추가하면서 도입된 정규화 효과와 표현력 증가의 조합으로 판단된다고 한다(아래 Figure 4). 또한, Figure1을 보면 random grow와 gradient growth간의 차이가 거의 없었음을 보였다.
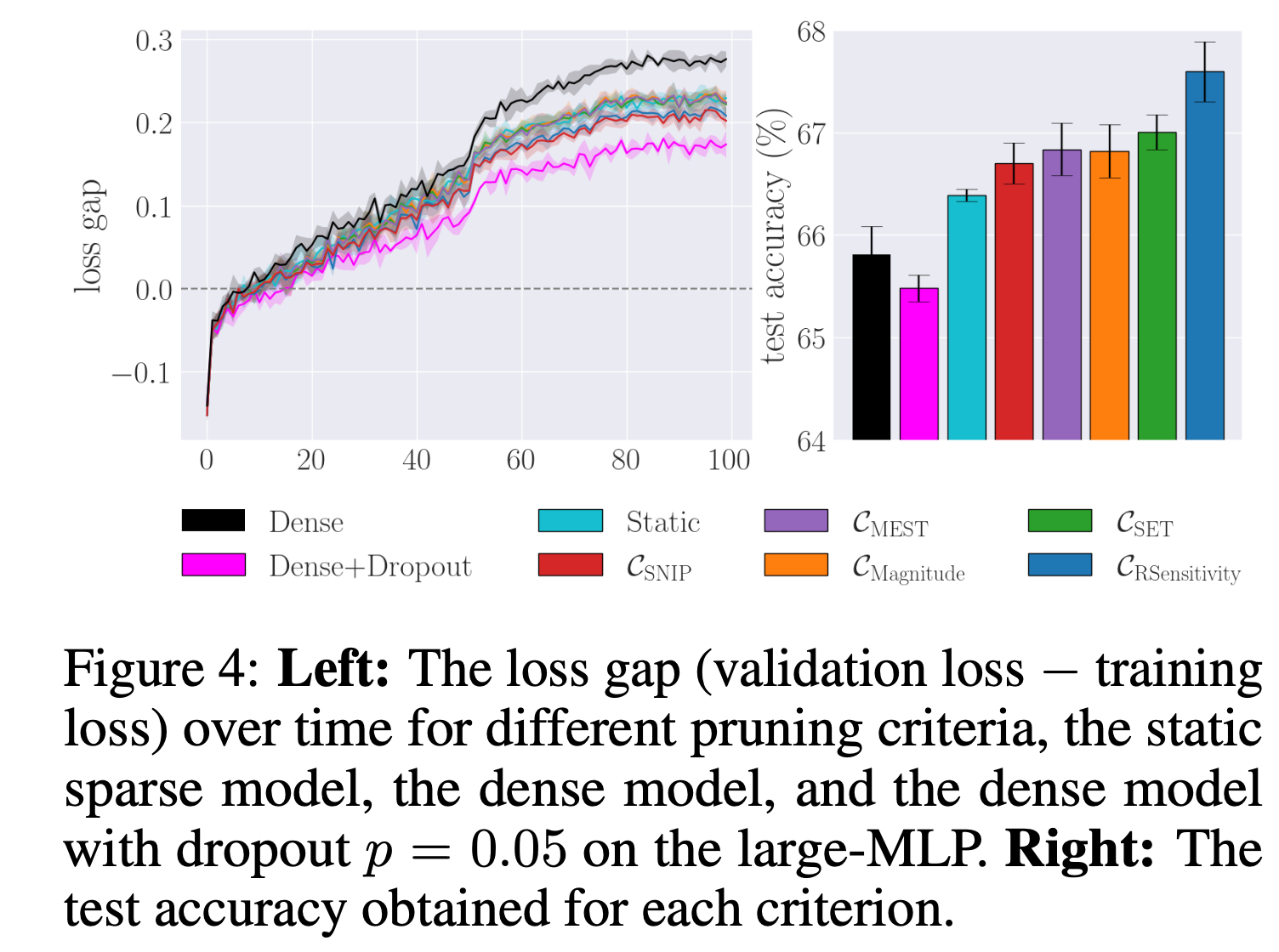
topology update frequency가 다양한 pruning 효과에 어떻게 영향을 미치는가?

Figure 5를 보면, MLP는 $\delta t$가 너무 작으면 성능이 떨어지는 것을 볼 수 있고, ramdom growing에 대해 최적의 업데이트 주기는 800이라고 이야기한다. gradient growing에서도 800은 좋은 결과를 보이지만, 1600이 더 좋아보인다고 이야기한다.
(800의 경우 batchsize 128기준으로 약 2epoch마다 업데이트 된다고 한다)
ResNet56에서도 6400 (16epoch마다 1번)도 좋은 성능을 보였지만, 아예 안하는 (static sparse training) 경우엔 성능이 떨어지는 것을 볼 수 있다. 또한, gradient growing에 작은 $\delta t$를 사용하게 되면 큰 성능저하가 발생하므로, 함께 사용하지 않거나 적절한 업데이트 주기를 찾는 것이 필요하다고 이야기한다.
논문의 저자들은 Figure 5를 토대로, 빈번하게(small $\delta t$)가 큰 의미가 없다고 이야기하며 몇번의 pruning -> regrowing만으로도 static initialization을 개선하기에 충분하다고 주장한다.
다양한 pruning criterion이 유사한 network topologies를 생성하는 정도는 어느 정도인가?
CIFAR10으로 sparse connectivity가 처음 update되는 순간을 분석했으며, 유사도 측정은 Jaccard index를 사용했다고 한다.

위 Figure 6를 보면, SET과 Magnitude가 주로 동일한 weight를 pruning한다는 것을 볼 수 있으며, 이는 양수와 음수 weight의 절대값이 비슷하다는 것을 말한다.
얕은 network(MLP, CNN)의 경우, MEST도 Magnitude와 거의 비슷한 구조를 생겅하지만, SNIP와 RSensitivity는 서로 다른 구조를 택하는 것을 볼 수 있다. SNIP는 score를 기울기의 크기로 곱하지만, RSensitivity는 그 역수를 사용하기 때문에 자연스러운 결과라고 저자들은 말한다.
이 실험을 토대로, Magnitude, SET, MEST와 같은 pruning criterion들이 유사한 sparse connectivity를 만든다는 것을 의미한다고 한다.
추가적으로, 각 pruning criterion이 찾은 최종 sprase구조의 유사성도 비교했는데, 이는 Figure 6의 (b)에서 볼 수 있다.
이러한 실험을 바탕으로, 성능 좋은 criterion들이 비슷한 mask를 만들지만, 효율적이지 않은 criterion과는 비교적 다른 것을 보였다.
이는 magnitude criterion이 다른 방법들과 실제로는 비슷하게 동작한다는 것을 의미한다고 말한다.
저자들은 마지막으로 DST에서 구조적 유사성 실험의 중요성 인식을 높이길 바란다며 논문을 마무리한다.
(baseline으로 magnitude깔고, 본인들의 ours를 보이면서 성능비교를하여 논문을 썼을텐데, 실제 weight가 선택되는 구조적인 실험은 진행하지 않았으며, 구조적인 실험결과 좋은 성능을 내는 애들은 magnitude와 큰 차이가 없더라, 앞으로는 구조적 유사성 실험도 추가했으면 좋겠다~ 라는 이야기 같다.)




